Why Is Eulers Formula For Polyhedron? Video
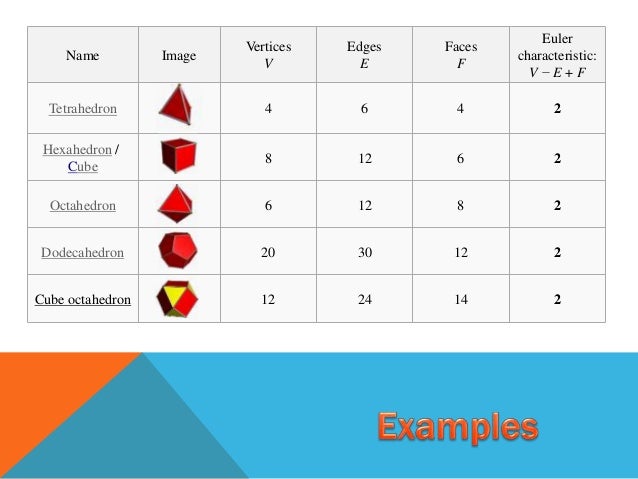
Platonic Solids 3D Polyhedrons To Verify Euler's Formula F + V - E = 2Was specially: Why Is Eulers Formula For Polyhedron?
| Why Is Eulers Formula For Polyhedron? | 1 day ago · polyhedral surface S which is triangulated with F triangles, with a total of E edges and V vertices in the triangulation, then the Euler characteristic is given by χ(S) = F −E +V. So we consider triangulations of surfaces F and G. A triangulation of quotient surface G can be picked so that the. 2 days ago · Why must an isotoxal polyhedron or tiling be isogonal or isohedral? 0 Prove that in any convex polyhedron, the number of faces that have an odd number of edges is even. 2 days ago · For the polyhedron, use Euler&#;s Formula to find the missing number. faces: edges: 16 vertices: 9 Get the answers you need, now! |
| Volunteering Personal Statement | 2 days ago · For the polyhedron, use Euler&#;s Formula to find the missing number. faces: edges: 16 vertices: 9 Get the answers you need, now! 2 days ago · Why must an isotoxal polyhedron or tiling be isogonal or isohedral? 0 Prove that in any convex polyhedron, the number of faces that have an odd number of edges is even. 1 day ago · Following the same formula as in the first example, we will then indemnify you: EUR 1, x 83% debt coverage x 90% policy indemnity = EUR In the end, the cost is reduced and instead of EUR 1,, you would only pay EUR + full VAT for the recovery of the EUR 12, debt (a cost of % of the amount collected). |
| Racial Discrimination In Mainstream Media | 13 hours ago · This preview shows page 1 - 4 out of 4 pages.. until it forms a point. Therefore, cone is not a polyhedron. Very sure 3. What is the value of f + v − e for a pentagonal prism? A. 1 B. 2 C. 4 D. 5 f= 7 v= 10 e= 15 f+v-e 7+= 2 4. A polyhedron has 12 vertices and 30 edges. 1 day ago · View PNG from MATH at University of Michigan. Euler's Formula: According to Euler's formula for any consent polyhedron. the number of Faces [F3 and yertices m added together is . 2 days ago · Why must an isotoxal polyhedron or tiling be isogonal or isohedral? 0 Prove that in any convex polyhedron, the number of faces that have an odd number of edges is even. |
Why Is Eulers Formula For Polyhedron? - And have
Why Dr. Johanna Budwig is a legendary figure in the world of natural approaches to treating cancer. She created a simple formula to defeat the disease. All you have to do is blend two common foods together. Sounds too good to be true? Boy, was I wrong. I was soon convinced this treatment is powerful and it works. For some people it really is that simple to defeat cancer.Conventions by extrinsic rotations[ edit ] Extrinsic rotations are elemental rotations that occur about the axes of the fixed coordinate system xyz. The Here system rotates, while xyz is fixed. Starting with XYZ overlapping xyz, a composition of three extrinsic rotations can be used to reach Fodmula target orientation for XYZ. In sum, the three elemental rotations occur about z, x and z.
Indeed, this sequence is often denoted z-x-z or Sets of rotation axes associated with both proper Euler angles and Tait—Bryan angles are commonly named using this notation see above for details. Signs, ranges and conventions[ edit ] Angles are commonly defined according to the right-hand rule.
Namely, they have positive values when they represent a rotation that appears clockwise when looking in the positive direction of the axis, and negative values when the rotation appears counter-clockwise. The opposite convention left hand rule is less frequently adopted.
Your Answer
These ambiguities are known as gimbal lock in applications. There are six possibilities of choosing the rotation axes for proper Euler angles. In all of them, the first and third rotation Wgy are the same. Intrinsic greenPrecession blue and Nutation red Precession uElers, nutationand intrinsic rotation spin are defined as the movements obtained by changing one of the Euler angles while leaving the other two constant. These motions are not expressed in terms of the external frame, or in terms of the co-moving rotated body frame, but in a mixture. They constitute a mixed axes of rotation system, where the first angle moves the line of nodes around the external axis z, the second rotates around the line of nodes N and the third one is an intrinsic rotation around Z, an axis fixed in Why Is Eulers Formula For Polyhedron?
body that moves. As an example, consider a top.
Navigation menu
The top spins around its own axis of symmetry; this corresponds to its intrinsic rotation. It also rotates around its pivotal axis, with its center of mass orbiting the pivotal axis; this rotation is a precession. Finally, the top can source up and down; the inclination angle is the nutation angle. The same example can be seen with the movements of the earth.
Logga in här
Though all three movements can be represented by a http://pinsoftek.com/wp-content/custom/summer-plan-essay/descriptive-essay-about-food-street.php operator with constant coefficients in some frame, they cannot be represented by these operators all at the same time. Given a reference frame, at most one of them will be coefficient-free. Only precession can be expressed in general as a matrix in the basis of the space without dependencies of the other angles.]
I apologise, but, in my opinion, you are not right. I can defend the position. Write to me in PM, we will communicate.
Yes, you have correctly told